在數學的世界裡,σ (sigma) 是一個非常重要的符號,它代表著「求和」的意思。簡單來說,當我們看到 σ 時,就表示接下來有一連串的數字需要我們加起來, 巫老師幫同學整理了有關 σ公式相關表格,來看下去吧!
閱讀更多:三角函數公式懶人包:Sin Cos Tan公式表大全
σ 公式表
下面這三個公式同學應該不陌生,n 代表的是數字有幾項,i 代表的是數列從 1 開始,同學需要注意的是 i 值必須從 1 開始。
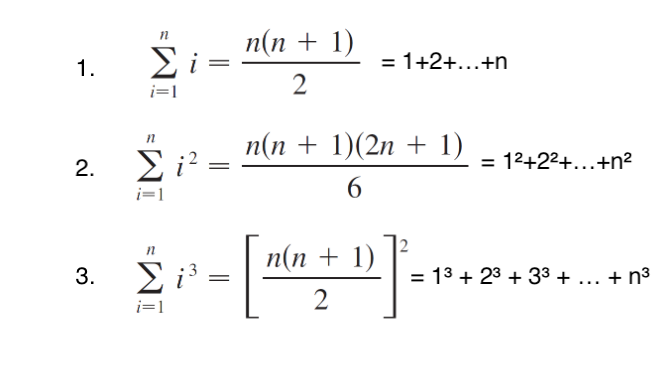
σ 公式在幹嘛?
σ 公式簡單來說就是在求和:
- Σ 後面會跟著一個表示式,這個表示式通常包含一個變數(例如i、k),以及一個表示式。
- Σ 的上方和下方會分別標示變數的起始值和終止值。
- 例如:Σ(i=1 to 5) i 就表示將1到5的所有整數加起來,也就是 1+2+3+4+5。
1. 算數級數
算數級數簡單來說是把一串等差的數相加,每一項與前一項的差都相等,這個相等的差稱為公差。
- σ 表示法:假設第一項為 a,公差為 d,則前 n 項的和可以用 σ 表示為:Σ(i=1 to n) (a + (i-1)d)。
- 舉例:求 1+3+5+7+9 的和,可以用 σ 表示為:Σ(i=1 to 5) (1 + 2(i-1))。
- 公式:算數級數的前 n 項和有公式:Sn = n/2 * (a + L),其中 L 為最後一項。
- 應用:計算等間隔時間內的工作量總和,以及等間隔排列的物體總數。
2. 等比級數
等比級數是一串數列,其中每一項與前一項的比值都相等,這個相等的比值稱為公比,而等比級數就是一串等比的數相加。
- σ 表示法:假設第一項為 a,公比為 r,則前 n 項的和可以用 σ 表示為:Σ(i=1 to n) (a * r^(i-1))
- 舉例:求 1+2+4+8+16 的和,可以用 σ 表示為:Σ(i=1 to 5) (1 * 2^(i-1))。
- 公式:等比級數的前 n 項和有公式:Sn = a * (1-r^n) / (1-r) (當r≠1時)。
- 應用:計算複利、折舊、分析人口成長、放射性衰變等現象。
3. 級數求和
級數求和是將無窮數列的項逐一相加所得到的和。
- σ表示法:用 σ 表示無窮級數時,上標通常寫成 ∞。
- 舉例:Σ(i=1 to ∞) (1/2^i) 表示1/2 + 1/4 + 1/8 + … 的和。
- 收斂與發散:不是所有的級數都有和,有些級數的和會趨近於一個特定的值(收斂),而有些級數的和會越來越大,沒有上限(發散)。
對 σ 公式還不了解嗎?
來讓巫老師幫你解決問題!巫老師擅長找出學生的個別弱點,改善學生讀書的方式,讓遇到大考多變的題型,也可以不死背公式解題!還在猶豫什麼?趕快來報名巫老師的家教課程吧!