考試快到了還在為三角函數苦惱嗎?有了這份 sin cos tan公式表,你的解題速度將大幅提升!我們整理了最常用的三角函數公式,還有搭配詳細的解說和範例,讓你輕鬆掌握解題技巧,一起往下閱讀吧!
閱讀更多:σ 公式統整大全,高中生必知的數學符號
三角函數定義
三角函數是一個描述角度與邊長之間關係的函數。我們通常在直角三角形中定義這些函數,將一個銳角的對邊、鄰邊和斜邊的比值分別定義為正弦(sine)、餘弦(cosine)和正切(tangent)。
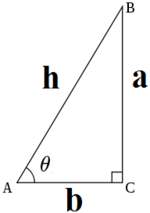
- 正弦 (sin): 對邊 / 斜邊
- 餘弦 (cos): 鄰邊 / 斜邊
- 正切 (tan): 對邊 / 鄰邊
除了上述三個基本函數外,還有餘切(cotangent)、正割(secant)和餘割(cosecant)等衍生函數,它們分別是正切、餘弦和正弦的倒數,但現在不會考了。
Sin cos tan公式表
以下幫同學整理了一下三角函數的公式表,包含商數關係、平方關係、餘角關係、補角關係和負角關係。
公式名稱 | 公式 | 備註 |
商數關係 | tanθ = sinθ / cosθ cotθ = cosθ / sinθ |
|
平方關係 | sin²θ + cos²θ = 1 1 + tan²θ = sec²θ 1 + cot²θ = csc²θ | |
餘角關係 | sin(90° – θ) = cosθ cos(90° – θ) = sinθ tan(90° – θ) = cotθ | |
補角關係 | sin(180° – θ) = sinθ cos(180° – θ) = -cosθ tan(180° – θ) = -tanθ | |
互角關係 | sin(-θ) = -sinθ cos(-θ) = cosθ tan(-θ) = -tanθ | |
和角公式 | sin(α + β) = sinα cosβ + cosα sinβ cos(α + β) = cosα cosβ – sinα sinβ tan(α + β) = (tanα + tanβ) / (1 – tanα tanβ) | |
差角公式 | sin(α – β) = sinα cosβ – cosα sinβ cos(α – β) = cosα cosβ + sinα sinβ tan(α – β) = (tanα – tanβ) / (1 + tanα tanβ) | |
倍角公式 | sin2θ = 2sinθ cosθ cos2θ = cos²θ – sin²θ = 2cos²θ – 1 = 1 – 2sin²θ tan2θ = 2tanθ / (1 – tan²θ) | |
半角公式 | sin(θ/2) = ±√[(1 – cosθ) / 2] cos(θ/2) = ±√[(1 + cosθ) / 2] tan(θ/2) = ±√[(1 – cosθ) / (1 + cosθ)] | |
疊合公式 | A sinθ + B cosθ = √(A² + B²) sin(θ + φ) | |
其他常用公式 |
|
三角函數的大小關係
以下先幫同學整理了θ 的範圍和sinθ 與 cosθ 的關係,在 0°~ 90° 的範圍內,sinθ 和 cosθ 的大小關係與角度 θ 有關:
- 當 θ 小於 45° 時,cosθ 大於 sinθ。
- 當 θ 等於 45° 時,sinθ 等於 cosθ。
- 當 θ 大於 45° 時,sinθ 大於 cosθ。
也順便整理了一個表格如下:
| θ 的範圍 | sinθ 與 cosθ 的關係 |
| 0° < θ < 45° | sinθ < cosθ |
| θ = 45° | sinθ = cosθ |
| 45° < θ < 90° | sinθ > cosθ |
圖像呈現:
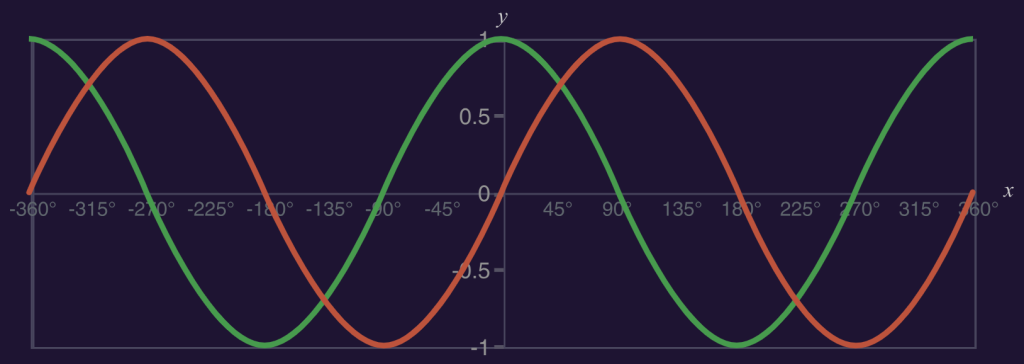
- 藍色曲線代表 sinθ 的函數圖形。
- 紅色曲線代表 cosθ 的函數圖形。
- 在 0° 到 45° 之間,藍色曲線在紅色曲線下方,表示 sinθ 的值小於 cosθ。
- 在 45° 時,兩條曲線交於一點,表示 sinθ 和 cosθ 的值相等。
- 在 45° 到 90° 之間,藍色曲線在紅色曲線上方,表示 sinθ 的值大於 cosθ。
為什麼會這樣?
1. 直角三角形解釋:
- 當角度 θ 很小時,對邊相對於斜邊較短,因此 sinθ 的值較小。
- 當角度 θ 接近 90° 時,對邊相對於斜邊較長,因此 sinθ 的值較大。
- cosθ 的變化趨勢正好與 sinθ 相反。
2. 單位圓解釋:
- 在單位圓上,隨著角度 θ 從 0° 增加到 90°,對應的點在單位圓上從 (1, 0) 移動到 (0, 1)。
- 在這個過程中,y 座標 (sinθ) 不斷增加,而 x 座標 (cosθ) 不斷減少。
- 當 θ = 45° 時,對應的點為 (√2/2, √2/2),此時 sinθ 和 cosθ 的值相等。
影響三角函數大小的因素
1. 角度的象限:
- 第一象限:所有三角函數值均為正。
- 第二象限:sinθ 為正,cosθ 和 tanθ 為負。
- 第三象限:tanθ 為正,sinθ 和 cosθ 為負。
- 第四象限:cosθ 為正,sinθ 和 tanθ 為負。
2. 角度的大小:
- 在同一個象限內,角度越大,sinθ一般越大(但不絕對),cosθ 一般越小(但不絕對)。
- tanθ 隨著角度的增大而單調遞增。
3. 例子:
- sin 30° < sin 60°
- cos 45° > cos 60°
- tan 30° < tan 45°
如果 θ 的角度越大,sinθ 和 tanθ 就會越大,但是 cosθ 會越小。
數A 數B 三角函數範圍
| 數A | 數B | |
| 弧度量 | ✓ | ✓ |
| sin 函數圖形 | ✓ (多考 cos, tan 函數圖形) | ✓ |
| 定義域、值域 | ✓ | ✕ |
| 週期性、週期現象數學模型 | ✓ | ✓ |
| 正餘弦函數的疊合 | ✓ | ✕ |
閱讀更多:【2024 最新】數A 數 B 內容與難度差異、數 B 科系,高二生要怎麼選?
公式背不起來怎麼辦?
巫老師高中數學家教能為你量身打造學習進度,從基礎觀念到進階解題,循序漸進引導你掌握考題的精髓。透過一對一的教學,巫老師能針對你的弱點加強,讓你快速提升數學成績!還在等什麼?趕快聯繫巫老師,讓數學不再是你的絆腳石!